Question

Find the length of AB. Leave

your answer in terms of 7.

A

20° AB = [ ? ]

27

1B

Enter

Answer 1

AB = 3π

Explanation:

See attachment for correct format of question.

Given

From the attachment, we have that

θ = 20°

Radius, r = 27

Required

Find length of AB

AB is an arc and it's length can be calculated using arc length formula.

`Length = (\theta)/(360) * 2\pi r`

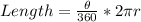
Substitute 20 for θ and 27 for r

`Length = (20)/(360) * 2\pi *27`

`Length = (20 * 2\pi * 27)/(360)`

`Length = (1080 \pi)/(360)`

`Length = 3\pi`

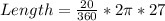
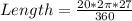
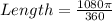
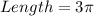
Hence, the length of arc AB is terms of π is 3π