Answer:
0.41
Explanation:
Given;
5.6, 5.2, 4.6, 4.9, 5.7, 6.4
To calculate the variance of a given set of ungrouped data, follow the following steps;
(i). First calculate the mean (average) of the data as follows;
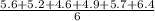 =
=
 = 5.4
= 5.4
(ii) Secondly, find the deviation of each point data from the mean as follows;
5.6 - 5.4 = 0.2
5.2 - 5.4 = -0.2
4.6 - 5.4 = -0.8
4.9 - 5.4 = -0.5
5.7 - 5.4 = 0.3
6.4 - 5.4 = 1.0
(iii) Thirdly, find the square of each of the results in step ii.
(0.2)² = 0.04
(-0.2)² = 0.04
(-0.8)² = 0.64
(-0.5)² = 0.25
(0.3)² = 0.09
(1.0)² = 1.0
(iv) Fourthly, find the sum of the results in step iii.
0.04 + 0.04 + 0.64 + 0.25 + 0.09 + 1.0 = 2.06
(v) The variance, v, is now the quotient of the result in step (iv) and n-1. i.e
v =
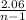
Where;
n = number of data in the set
n = 6 in this case
Therefore,
v =
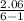
v =
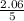
v = 0.412
Therefore, the variance is 0.41 to the nearest hundredth