Question

Find the area of the segment of circle c shown above. A. Asegment= 353.66 B. Asegment= 434.88 C. Asegment= 458.88 D. Asegment= 707.32 (It's not B, C, or D. However, I don't know how it is A)

Answer 1

Option (B)

Explanation:

Area of sector of a circle =
`(\theta)/(360)(\pi r^(2) )`

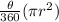
where r = radius of the circle

θ is the central angle subtended by the arc TS.

Area of the given sector =
`(120)/(360)(\pi) (24^(2) )`

=
`(576\pi )/(3)`

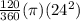
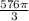
= 192π

= 603.19 unit²

Area of the triangle (not shaded) =
`(1)/(2)(\text{TC})(\text{CS})\text{sin}(120)`

=
`(1)/(2)(24)(24)(\text{sin}120)`

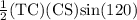
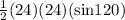
= 167.22 unit²

Area of the shaded area = Area of the sector - Area of triangle

= 603.19 - 167.22

= 435.96 unit²

Therefore, the area of the shaded region = 435.96 unit²

The nearest value of the area has been given in Option (B).

So Option B will be the answer.