Question

Use z scores to compare the given values. In a recent awards​ ceremony, the age of the winner for best actor was 34 and the age of the winner for best actress was 62. For all best​ actors, the mean age is 43.4 years and the standard deviation is 8.8 years. For all best​ actresses, the mean age is 38.2 years and the standard deviation is 12.6 years.​ (All ages are determined at the time of the awards​ ceremony.) Relative to their​ genders, who had the more extreme age when winning the​ award, the actor or the​ actress? Explain.

Answer 1

The actress had more extreme age when winning the​ award.

Explanation:

We are given that for all the best​ actors, the mean age is 43.4 years and the standard deviation is 8.8 years. For all best​ actresses, the mean age is 38.2 years and the standard deviation is 12.6 years.

To find who had the more extreme age when winning the​ award, the actor or the​ actress, we will use the z-score method.

• Finding the z-score for the actor;

Let X = age of the winner for best actor

The z-score probability distribution for the normal distribution is given by;

Z =
`(X-\mu)/(\sigma)` ~ N(0,1)

where,
`\mu` = mean age = 43.4 years

`\sigma` = standard deviation = 8.8 years

It is stated that the age of the winner for best actor was 34, so;

z-score for 34 =
`(X-\mu)/(\sigma)`

=
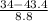`(34-43.4)/(8.8)` = -1.068

• Finding the z-score for the actress;

Let Y = age of the winner for best actress

The z-score probability distribution for the normal distribution is given by;

Z =
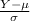`(Y-\mu)/(\sigma)` ~ N(0,1)

where,
`\mu` = mean age = 38.2 years

`\sigma` = standard deviation = 12.6 years

It is stated that the age of the winner for best actress was 62, so;

z-score for 62 =
`(Y-\mu)/(\sigma)`

=
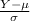
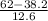`(62-38.2)/(12.6)` = 1.889

Since the z-score for the actress is more which means that the actress had more extreme age when winning the​ award.