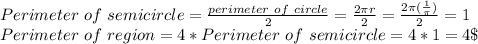Question

A region is bounded by semicircular arcs constructed on the side of a square whose sides measure 2/\pi, as shown. What is the perimeter of this region?

Answer 1

4

Explanation:

The perimeter of the region is equal to the sum of the perimeter of the four semicircular arc. Since the semicircular arcs have the same measure, therefore:

Perimeter of region = 4 × Perimeter of semicircular arc.

The side of the square = diameter of the semicircle = 2/π.

The radius of semicircle = diameter/2 =
`(2/\pi)/(2) =(1)/(\pi)`

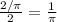
The perimeter of a semicircle = perimeter of a circle ÷ 2

`Perimeter\ of \ semicircle = (perimeter\ of\ circle)/(2)=(2\pi r)/(2)=(2\pi ((1)/(\pi) ))/(2) =1\\ Perimeter\ of\ region = 4*Perimeter\ of \ semicircle=4*1=4\`