Question

Beth is knitting mittens and gloves. Each pair must be processed on three machines. Each pair of mittens requires 2 minutes on Machine A, 2 minutes on Machine B, and 4 minutes on Machine C. Each pair of gloves requires 4 minutes on Machine A, 2 minutes on Machine B, and 1 minute on Machine C. Machine A, B, and C are available 32, 18, and 24 minutes, respectively, everyday. The profit on a pair of mittens is $8.00 and on a pair of gloves is $10.00.

Answer 1

Two mittens and seven gloves

Explanation:

I presume you are asking how many mittens and how many gloves Beth should knit to produce the most profit.

Let x = the number of mittens and

Let y = the number of gloves

1. Summarize the information in a table

`\begin{array}{cccc}&\textbf{Mittens}& \textbf{ Gloves} & \textbf{Minutes Available}\\\text{Machine A} & 2 & 4 & 32\\\text{Machine B} & 2 & 2 & 18\\\text{Machine C} & 4 & 1 & 24\\\text{Unit profit} & $8.00 & $10.00 & \\\end{array}`

2. List the constraints

(a) Beth can't make a negative number of mittens, so

x ≥ 0.

(b) Neither can she make a negative number of gloves, so

y ≥ 0.

(c) The total number of minutes on Machine A cannot exceed 32, so

2x + 4y ≤ 32.

(d) The total number of minutes on Machine B cannot exceed 18, so

2x + 2y ≤ 18.

(e) The total number of minutes on Machine C cannot exceed 24, so

4x + y ≤ 24.

3. Write an equation for the profit

P = 8.00x + 10.00y

4. Graph the constraints to identify the feasible region

See the figure below. The feasible region is the dark green area where all three regions overlap.

5. Determine the points of intersection between the constraints

(i) Constraints (c) and (d)

`\begin{array}{rcr}2x + 4y & = & 32\\2x + 2y & = & 18\\2y & = & 14\\y & = & \mathbf{7}\\2x + 14 & = & 18\\2x & = &4\\x & = & \mathbf{2}\\\end{array}\\`

The lines intersect at (2,7).

(ii) Constraints (c) and (e)

`\begin{array}{rcl}2x + 4y & = & 32\\4x + y & = & 24\\4x + 8y & = & 64\\7y & = & 40\\y & = & \mathbf{(40)/(7)}\\\\4x + (40)/(7) & = & 24\\\\4x & = &24 - (40)/(7)\\\\4x & = & (128)/(7)\\\\x & = & \mathbf{(32)/(7)}\\\\\end{array}\\`

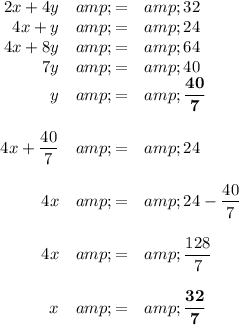
The lines intersect at (27/7,32/7).

(iii) Constraints (d) and (e)

`\begin{array}{rcr}2x + 2y & = & 18\\4x + y & = & 24\\4x + 4y & = & 36\\3y & = & 12\\y & = & \mathbf{4}\\4x +4 & = & 24\\4x & = &20\\x & = & \mathbf{5}\\\end{array}\\`

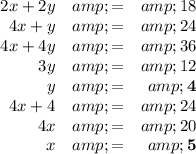
The lines intersect at (5,4).

6. Determine the x- and y-intercepts of the feasible region

(i) x-intercept

`\begin{array}{rcr}4x + y & = & 24\\4x + 0 & = & 24\\x & = & \mathbf{6}\\\end{array}`

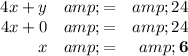
The x-intercept is at (6,0).

(ii) y-intercept

`\begin{array}{rcr}2x + 4y & = &32\\2(0) + 4y & = &32\\4y & = & 32\\y & = & \mathbf{8}\\\end{array}`

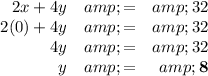
The y-intercept is at (0,8).

The five black dots are the vertices of the polygon that represents the feasible region.

7. Calculate the maximum profit

Calculate the profit at each of the vertices.

(i) At (0,0)

P = 8.00x + 10.00y = 8.00(0) + 10.00(0) = 0 + 0 = $0

(ii) At (2,7)

P = 8.00(2) + 10.00(7) = 16 + 70 = $86

(iii) At (5,4)

P = 8.00(5) + 10.00(4) = 40 + 40 = $80

(iv) At (6,0)

P = 8.00(6) + 10.00(0) = 48 + 0 = $48

The maximum profit occurs at (2,7)

Thus, Beth should knit two mittens and seven gloves.