Question

Approximate the stationary matrix S for the transition matrix P by computing powers of the transition matrix P. Pequalsleft bracket Start 2 By 2 Matrix 1st Row 1st Column 0.38 2nd Column 0.62 2nd Row 1st Column 0.24 2nd Column 0.76 EndMatrix right bracket

Answer 1

The stationary matrix is:

S = [0.2791, 0.7209]

Explanation:

The transition matrix, P is:

`P=\left[\begin{array}{cc}0.38&0.62\\0.24&0.76\end{array}\right]`

The stationary matrix S for the transition matrix P would be obtained by computing k powers of P until all the two rows of P are identical.

Compute P² as follows:

`P^(2)=\left[\begin{array}{cc}0.38&0.62\\0.24&0.76\end{array}\right]* \left[\begin{array}{cc}0.38&0.62\\0.24&0.76\end{array}\right]`

`=\left[\begin{array}{cc}0.2932&0.7068\\0.2736&0.7264\end{array}\right]`

Compute P³ as follows:

`P^(3)=P^(2)* P`

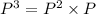
`=\left[\begin{array}{cc}0.2932&0.7068\\0.2736&0.7264\end{array}\right]* \left[\begin{array}{cc}0.38&0.62\\0.24&0.76\end{array}\right]\\\\=\left[\begin{array}{cc}0.2810&0.7190\\0.2783&0.7217\end{array}\right]`

Compute P⁴ as follows:

`P^(4)=P^(3)* P`

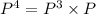
`=\left[\begin{array}{cc}0.2810&0.7190\\0.2783&0.7217\end{array}\right]* \left[\begin{array}{cc}0.38&0.62\\0.24&0.76\end{array}\right]\\\\=\left[\begin{array}{cc}0.2793&0.7207\\0.2790&0.7210\end{array}\right]`

Compute P⁵ as follows:

`P^(5)=P^(4)* P`

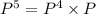
`=\left[\begin{array}{cc}0.2793&0.7207\\0.2790&0.7210\end{array}\right]* \left[\begin{array}{cc}0.38&0.62\\0.24&0.76\end{array}\right]\\\\=\left[\begin{array}{cc}0.2791&0.7209\\0.2791&0.7209\end{array}\right]`

For k = 5, we get both the rows identical.

The stationary matrix is:

S = [0.2791, 0.7209]