Question

Evaluate the spherical coordinate integral

u=x+y , v= -2x + y;

∫ ∫ (-3x + 4y) dx dy
R

where R is the parallelogram bounded by the lines y = -x + 1, y = -x + 4, y = 2x + 2, y = 2x + 5

Answer 1

Rewrite the equations of the given boundary lines:

y = -x + 1 ==> x + y = 1

y = -x + 4 ==> x + y = 4

y = 2x + 2 ==> -2x + y = 2

y = 2x + 5 ==> -2x + y = 5

This tells us the parallelogram in the x-y plane corresponds to the rectangle in the u-v plane with 1 ≤ u ≤ 4 and 2 ≤ v ≤ 5.

Compute the Jacobian determinant for this change of coordinates:

`J=\begin{bmatrix}(\partial u)/(\partial x)&(\partial u)/(\partial y)\\(\partial v)/(\partial x)&(\partial v)/(\partial y)\end{bmatrix}=\begin{bmatrix}1&1\\-2&1\end{bmatrix}\implies|\det J|=3`

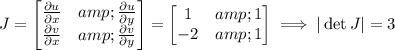
Rewrite the integrand:

`-3x+4y=-3\cdot\frac{u-v}3+4\cdot\frac{2u+v}3=\frac{5u+7v}3`

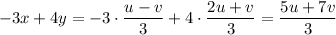
The integral is then

`\displaystyle\iint_R(-3x+4y)\,\mathrm dx\,\mathrm dy=3\iint_(R')\frac{5u+7v}3\,\mathrm du\,\mathrm dv=\int_2^5\int_1^45u+7v\,\mathrm du\,\mathrm dv=\boxed{333}`