Question

Find the length of segment JK. (Enter the just the value, without any units.)

Answer 1

8

Explanation:

From the figure, <LJK =~ <LPM , also, <JLK =~ <PLM because vertical angles are congruent.

By Angle - Angle (AA) Similarity postulate, of two angles of a triangle are congruent to two angles of another triangle , then the triangles are similar.

Hence, ∆JLK ~ ∆PLM

Use the corresponding side lengths to write a proportion.

`(jl)/(pl) = (jk)/(pm)`

`(4)/(6) = (x)/(12)`

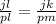
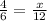
Apply cross product property

`6 * x = 12 * 4`

`6x = 48`

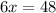
Divide both sides of the equation by 6

`(6x)/(6) = (48)/(6)`

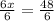
Calculate

`x = 8`

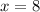
Since, JK = x then,

JK = 8

hope this helps...

Good luck on your assignment...

Answer 2

x = 8

Explanation:

Since we know that the 2 triangles are similar (AA Similarity), we find the ratio of Triangle PLM: 2

We then multiply 4 by 2 (the ratio) to get x = 8 as length JK.