Answer:
a) The heavier piece has a translational kinetic energy of 4647.857 joules, b) The lighter piece has a translational kinetic energy of 2582.143 joules.
Step-by-step explanation:
a) The object breaking can be described by means of the Principle of Energy Conservation, knowing that heavier piece has 1.8 times the mass of the lighter (
 ), both are modelled as particle due to the absence of rotation and that energy liberated by explosion is transform into kinetic energy, the equation that describes the phenomenon is:
), both are modelled as particle due to the absence of rotation and that energy liberated by explosion is transform into kinetic energy, the equation that describes the phenomenon is:
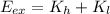
Where:
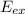 - Energy liberated by the explosion, measured in joules.
- Energy liberated by the explosion, measured in joules.
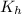 ,
,
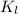 - Translational kinetic energies of the heavier and lighter piece, respectively.
- Translational kinetic energies of the heavier and lighter piece, respectively.
This expression is expanded by using the definition of translational kinetic energy and supposing the both parts are liberated at the same initial speed (
 ). Then:
). Then:
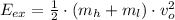
As can be seen, the energy liberated by expression is directly proportional to the mass of the system. Hence, the kinetic energy can be estimated by simple rule of three:
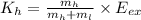
If
 and
and
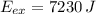 , then:
, then:
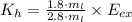
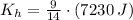
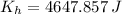
The heavier piece has a translational kinetic energy of 4647.857 joules.
b) The translational kinetic energy of the lighter piece is calculated by using the equation derived from the Principle of Energy Conservation:
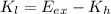
Given that
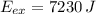 and
and
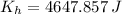 , the translational kinetic energy of the lighter piece is:
, the translational kinetic energy of the lighter piece is:
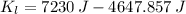
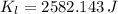
The lighter piece has a translational kinetic energy of 2582.143 joules.