Answer:
a)
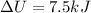
b)
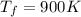
Step-by-step explanation:
a) To find the change in its internal energy (U) we need to use the following equation:
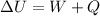
Where:
W: is the work done on the system
Q: is the energy transferred into the system by heat = 12.5 kJ
Since we have an isobaric expansion, the work is:
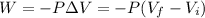
Where:
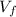 : is the final volume = 3.00 m³
: is the final volume = 3.00 m³
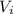 : is the initial volume = 1.00 m³
: is the initial volume = 1.00 m³
P: is the pressure = 2.50 kPa
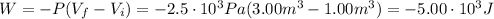
Now, we can find the change in its internal energy:
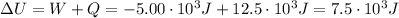
b) The final temperature can be found as follows:

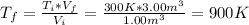
Hence, the final temperature is 900 K.
I hope it helps you!