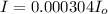Answer:
a
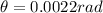
b
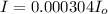
Step-by-step explanation:
From the question we are told that
The wavelength of the light is
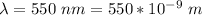
The distance of the slit separation is
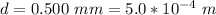
Generally the condition for two slit interference is
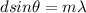
Where m is the order which is given from the question as m = 2
=>
![\theta = sin ^(-1) [(m \lambda)/(d) ]](https://img.qammunity.org/2021/formulas/physics/college/tdeh2gplmoo6dfxlsfmi988xxbrnnwppny.png)
substituting values
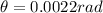
Now on the second question
The distance of separation of the slit is

The intensity at the the angular position in part "a" is mathematically evaluated as
![I = I_o [(sin \beta)/(\beta) ]^2](https://img.qammunity.org/2021/formulas/physics/college/x70wdhbu109o6oq6vnovleh8cv4pat9u42.png)
Where
 is mathematically evaluated as
is mathematically evaluated as
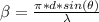
substituting values
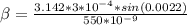
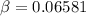
So the intensity is
![I = I_o [(sin (0.06581))/(0.06581) ]^2](https://img.qammunity.org/2021/formulas/physics/college/8hvjlma97li1alaxqe3uglz39sw5wlxk49.png)