Question

The number of deaths by road as recorded in a country is 2 per 50,000 of the population. Find the probability that in a town of 100,000 inhabitants within the country (a). between one and three inclusive, and (b). between two and five deaths by road will be recorded.

Answer 1

(a) 0.635

(b) 0.498

Explanation:

(a) The probability distribution is calculated using the cumulative distribution function of the Poisson as follows;

CDF =
`F(x)=e^(-\lambda t)\sum_(i = 0)^(\left | x \right |)(\lambda t^(i))/(i!)`

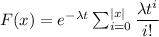
For x = three we have;

CDF = 0.781

For x = one we have;

CDF = 0.1465

Therefore, the probability that between one and three inclusive = 0.781 - 0.1465 = 0.635

(b) For x = 2 we have;

CDF = 0.4395

For x = one we have;

CDF = 0.9378

Therefore, the probability that between one and three inclusive = 0.9378- 0.4395= 0.498