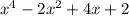Answer: k = 4
Explanation:
For this division, to determine the value of k, use the Remainder Theorem, which states that:
polynomial p(x) = dividend (x-a) * quotient Q(x) + remainder R(x)
Knowing the degree of quotient is
degree of Q = degree of p(x) - degree of (x-a)
For this case, Q(x) is a third degree polynomial.
Using the theorem:
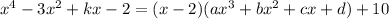

a = 1
b - 2a = 0 ⇒ b = 2
c - 2b = -3 ⇒ c = 1
-2d + 10 = -2 ⇒ d = 6
d - 2c = k ⇒ k = 4
Therefore, k = 4 and Q(x) =