Answer:
 .
.
Explanation:
It is given that the sum of first two terms of an infinite GP is 6.
nth term of a GP is
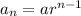
 ...(1)
...(1)
Each term is 5 times the sum of the succeeding terms.
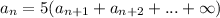
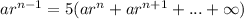
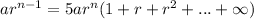
Divide both sides by a.
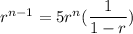
![[\text{Sum of infinite GP}=(a)/(1-r)]](https://img.qammunity.org/2021/formulas/mathematics/high-school/eebkgo2omqffs0captpx1wpgkgprj428uw.png)
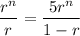
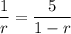
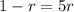

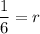
The common ratio is 1/6.
Put r=1/6 in (1).
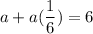
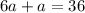
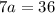

Second term
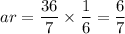
Therefore, the second term is
 .
.