Answer:
The answer is below
Explanation:
The equation of the line passing through two points is given by:
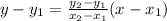
The equation of line AB is:
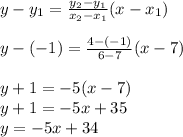
The midpoint of two lines is given as:
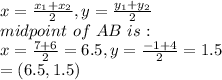
The equation of line AC is:
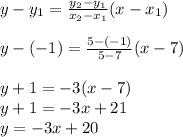
The midpoint of two lines is given as:
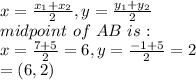
The product of the slope of a perpendicular bisector of a line and the slope of the line is -1. That is m1m2 = -1
The slope of the perpendicular bisector of AB is:
m(-5)=-1
m=1/5
The equation of the perpendicular bisector of AB passing through (6.5,1.5) is:

The slope of the perpendicular bisector of AB is:
m(-3)=-1
m=1/3
The equation of the perpendicular bisector of AB passing through (6,2) is:
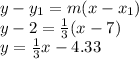
2) The point of intersection is gotten by solving y = 1/5 x -8.25 and y = 1/3 x-4.33 simultaneously.
Subtracting the two equations from each other gives:
0= -0.133x - 3.92
-0.133x = 3.92
x = -29.5
Put x = -29.5 in y = 1/5 x -8.25 i.e:
y = 1/5 (29.5) -8.25
y = -14.16
The point of intersection is (-29.5, -14.16)