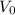Question

A parallel-plate capacitor C is charged up to a potential V0 with a charge of magnitude Q0 on each plate. It is then disconnected from the battery, and the plates are pulled apart to twice their original separation.

A. What is the new capacitance in terms of C?
B. How much charge is now on the plates in terms of Q_0 ?
C. What is the potential difference across the plates in terms of V_0

Answer 1

A. The new capacitance is half in term of C

B. The charge remains the same in terms of
`Q_(0)`

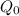
C. The potential difference is double in terms of
`V_(0)`

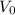
Step-by-step explanation:

The battery with a voltage of
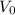`V_(0)` is used to charge the plates, giving it a capacitance of C.

The charging process leaves a charge of magnitude
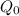`Q_(0)` on the plate

The battery is disconnected (this will leave it with a constant charge
`Q_(0)`)

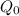the relationship between the charge, voltage and capacitance of the plate is

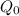`Q_(0)` = C
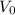`V_(0)` ......... equ 1

A. The relationship between capacitance and the distance of the plate is given as

C = Aε/d ......... equ 2

where A is the area of the plate,

ε is the permeability of free space,

d is the distance between the plates

The area of the plate does not change, and permeability of free space is a constant. The combination of all these means that if the distance is doubled, then the capacitance will be halved. This is from equ 2 when the distance becomes 2d, then we have

C' = Aε/2d

==> C' = C/2

B. Since the battery is disconnected, and the capacitor is not discharged, the charge on the plate will remains the same as
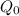`Q_(0)`. This is due to the conservation of charges.

C. Since the charge remains constant, and the capacitance is halved, then from equ 1, the new potential difference V will become double of the initial potential difference
`V_(0)`

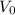
==> V = 2
`V_(0)`