Answer:
Las inecuaciones que pueden ayudar a calcular cuantos litros de pintura blanca se pueden tener como son
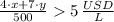 y
y
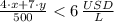 .
.
Explanation:
Esta situación puede ser descrita mediante una ecuación y una inecuación simultánea. La ecuación es de la capacidad del tanque, mientras que la inecuación es del coste unitario de la mezcla. Sean
 y
y
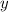 las capacidades empleadas de pintura blanca y pintura azul en litros, entonces:
las capacidades empleadas de pintura blanca y pintura azul en litros, entonces:
Capacidad del tanque (en litros)
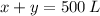
Coste unitario de la mezcla (en dólares por litro)
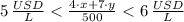
Es decir:
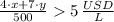 y
y
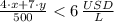
Las inecuaciones que pueden ayudar a calcular cuantos litros de pintura blanca se pueden tener como son
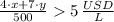 y
y
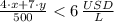 .
.