Question

Find the equation of the given parabola in vertex and standard form. Describe in words all transformations that have been applied to the graph of y=x^2 to obtain the given graph of the transformed function

Answer 1

Answer:
`a)\ \text{Vertex}:y=-(3)/(2)(x+1)^2+6`

`b)\ \text{Standard}:y=-(3)/(2)x^2-3x=(9)/(2)`

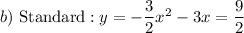
c) Transformations: reflection over the x-axis,

vertical stretch by a factor of 3/2,

horizontal shift 1 unit to the left,

vertical shift 6 units up

Explanation:

Intercept form: y = a(x - p)(x - q)

Vertex form: y = a(x - h)² + k

Standard form: y = ax² + bx + c

We can see that the new vertex is (-1, 6). Use the Intercept form to find the vertical stretch: y = a(x - p)(x - q) where p, q are the intercepts.

p = -3, q = 1, (x, y) = (-1, 6)

a(-1 + 3)(-1 -1) = 6

a (2)(-2) = 6

a = -6/4

a = -3/2

a) Input a = -3/2 and vertex (h, k) = (-1, 6) into the Vertex form to get:

`y=-(3)/(2)(x+1)^2+6`

b) Input a = -3/2 into the Intercept form and expand to get the Standard form:

`y=-(3)/(2)(x+3)(x-1)\\\\\\y=-(3)/(2)(x^2+2x-3)\\\\\\y=-(3)/(2)x^2-3x+(9)/(2)`

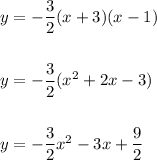
c) Use the Vertex form to identify the transformations:

`y=-(3)/(2)(x+1)^2+6`

• a is negative: reflection over the x-axis
• |a| = 3/2: vertical stretch by a factor of 3/2
• h = -1: horizontal shift left 1 unit
• k = +6: vertical shift up 6 units