Question

The equation of a circle is (x – 3)2 +(+8)2 = 36. Relative to the standard equation of a circle (zº+y? = r?), how has

this circle been shifted? What is the radius of the circle?
A. The circle has been shifted 3 units to the right and 8 units down.
= 6
B. The circle has been shifted 3 units to the left and 8 units down.
r=6
C. The circle has been shifted 8 units to the left and 3 units up.
r = 36
D. The circle has been shifted 3 units to the left and 8 units up.
r = 36
Please select the best answer from the choices provided
A
B

Answer 1

A. The circle has been shifted 3 units to the right and 8 units down, r=6

Explanation:

Recall that the equation of a circle is
`(x-h)^2+(y-k)^2=r^2` where
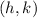`(h,k)` is the center of the circle and
`r` is the radius.

Given that the equation is
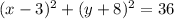`(x-3)^2+(y+8)^2=36`, this tells us that the center of the circle is at
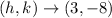`(h,k)\rightarrow(3,-8)` and the radius is
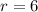`r=6`. Since the value of
`h` represents the amount of horizontal shift from the origin and
`k` represents the amount of vertical shift from the origin, then the circle was shifted 3 units to the right and 8 units down.