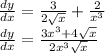Question

3√x -2/x^2

please show step by step of differentiation before combining the terms. ​

Answer 1

Explanation:

Before we differentiate, let us assign a variable to the function. Let y be equal to the function i.e let y = 3√x -2/x²

In differentiation if
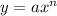`y = ax^(n)`, then
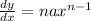`(dy)/(dx) = nax^(n-1)` where n is a constant and dy/dx means we are differentiating the function y with respect to x.

Applying the formula o the question given;

`y= 3√(x) -2/x^2\\y = 3{x}^(1)/(2) - 2x^(-2) \\\\`

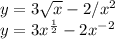
On differentiating the resulting function;

`(dy)/(dx) = (1)/(2)*3x^{(1)/(2)-1 } - (-2)x^(-2-1) \\\\(dy)/(dx) = (1)/(2)*3x^{-(1)/(2)} + 2x^(-3)\\ \\(dy)/(dx) = (1)/(2)*{\frac{3}{x^{(1)/(2) } }} + (2)/(x^(3) ) \\\\(dy)/(dx) = {\frac{3}{2x^{(1)/(2) } }} + (2)/(x^(3) )\\\\(dy)/(dx) = {(3)/(2√(x) )} + (2)/(x^(3) )`

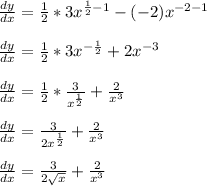
To combine the terms, we will add up by finding their LCM.

`(dy)/(dx) = {(3)/(2√(x) )} + (2)/(x^(3) )\\(dy)/(dx) = (3x^3+4√(x) )/(2x^(3) √(x))`