Answer:
The ratio of the time period of object 1 to the time period of object 2 is
 . (T₁ : T₂) = 1 : 4
. (T₁ : T₂) = 1 : 4
Step-by-step explanation:
Let suppose that both objects are moving along the circular paths at constant speed, such that period of rotation of each object is represented by the following formula:

Where:
 - Angular speed, measured in radians per second.
- Angular speed, measured in radians per second.
 - Period, measured in seconds.
- Period, measured in seconds.
The period is now cleared:
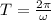
Angular speed (
 ) and linear speed (
) and linear speed (
 ) are related to each other by this formula:
) are related to each other by this formula:
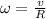
Where
 is the radius of rotation, measured in meters.
is the radius of rotation, measured in meters.
The angular speed can be replaced and the resultant expression is obtained:
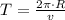
Which means that time period is directly proportional to linear speed and directly proportional to radius of rotation. Then, the following relationship is constructed and described below:
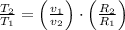
Where:
 ,
,
 - Time periods of objects 1 and 2, measured in seconds.
- Time periods of objects 1 and 2, measured in seconds.
 ,
,
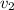 - Linear speed of objects 1 and 2, measured in meters per second.
- Linear speed of objects 1 and 2, measured in meters per second.
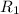 ,
,
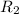 - Radius of rotation of objects 1 and 2, measured in meters.
- Radius of rotation of objects 1 and 2, measured in meters.
If
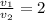 ,
,
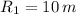 and
and
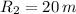 , the ratio of time periods is:
, the ratio of time periods is:
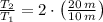
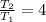
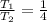
The ratio of the time period of object 1 to the time period of object 2 is
 .
.