Question

Find the zeros of ply nomial x2-3 and verify the relation ship

Answer 1

`x=\pm √(3)`

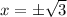
Explanation:

Consider the given polynomial is

`P(x)=x^2-3`

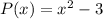
We need to find the zeros of the given polynomial.

Now,

`P(x)=0`

`x^2-3=0`

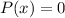
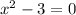
Add 3 on both sides.

`x^2=3`

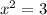
Taking square root on both sides.

`x=\pm √(3)`

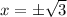
Therefore, zeros of the polynomial P(x) are
`-√(3) \text{ and }√(3)`.

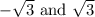To verify the relationship, put
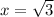`x=√(3)` in P(x).

`P(√(3))=(√(3))^2-3=3-3=0`

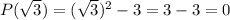
Put
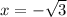`x=-√(3)` in P(x).

`P(-√(3))=(-√(3))^2-3=3-3=0`

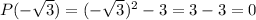
Since P(x)=0 for both values, therefore relationship verified.