Answer:
Explanation:
If the parabola is 72 m wide, then if we were to plot this parabola on a piece of (very large, lol) graph paper, we could plot one point at (72, 0) and the other one at (0, 0) since that would ensure that the arch is 72 m wide (72 - 0 = 72). The thing to remember now is that the vertex is exactly halfway between those 2 points with regards to the x-intercepts. In other words, if the width of the arch is 72 meters and the x values run from 0 to 72, then the x coordinate (or h, actually) of the vertex is 36 since 36 is halfway between 0 and 72 on the x-axis. Since the vertex goes up to 27 m, the k coordinate of the vertex is 27.
So here's what we have:
Coordinate points: (0, 0) and (72, 0)
Vertex: (36, 27)
We will use one of those coordinates along with the vertex in
 and solve for a. Pro tip: since this is an upside down parabola, a better be negative when we solve for it!
and solve for a. Pro tip: since this is an upside down parabola, a better be negative when we solve for it!
Filling in x, y, h, and k:
 and
and
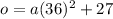 and
and
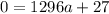 and
and
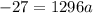 so
so
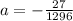 which simplifies to
which simplifies to
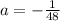
Writing the equation now looks like this:
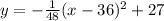
Not sure what form you need that expressed in, but that's the vertex form so it should work, considering you were given a vertex to work with.