Answer: Choice A. P = 1000M
===========================================================
Step-by-step explanation:
Use the log rule
log(A/B) = log(A) - log(B)
this works for any valid log base
So we can say
- log(P/N) = log(P) - log(N)
- log(M/N) = log(M) - log(N)
meaning that
- log(P/N) = 8 turns into log(P) - log(N) = 8
- log(M/N) = 5 turns into log(M) - log(N) = 5
We have this system of equations
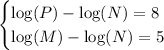
Subtract the equations straight down. You'll find the log(N) terms cancel out and we have the new equation log(P) - log(M) = 3 which transforms into log(P/M) = 3
Lastly, convert the log equation into its exponential equivalent form using the idea that log(b,x) = y turns into y = b^x, where b is the base
Throughout this problem, the base wasn't given. Instead its implied we're talking about base 10.
So,
log(P/M) = 3
P/M = 10^3
P/M = 1000
P = 1000M
-------------------------------------
Alternatively,
log(P/N) = 8 turns into P/N = 10^8
log(M/N) = 5 turns into M/N = 10^5
meaning that we can divide the two equations to get P/M = (10^8)/(10^5). That simplifies to P/M = 1000 and rearranges to P = 1000M