Question

Estimate the local maximum of...

Answer 1

Option A.

Explanation:

The given equation is

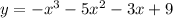`y=-x^3-5x^2-3x+9` ...(1)

We need to find the local maximum.

Differentiate the given equation w.r.t. x.

`y=-(3x^(3-1))-5(2x^(2-1))-3(1)+0`

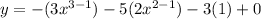
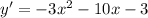`y'=-3x^2-10x-3` ...(2)

Now, equate y'=0 to find the extrem points.

`-3x^2-10x-3=0`

`-3x^2-9x-x-3=0`

`-3x(x+3)-1(x+3)=0`

`-(3x+1)(x+3)`

`3x+1=0\Rightarrow x=-(1)/(3)`

`x+3=0\Rightarrow x=-3`

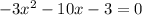
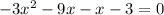
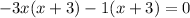
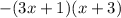
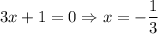
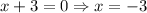
Differentiate (2) w.r.t. x.

`y''=-6x-10`

For
`x=-(1)/(3)`,

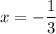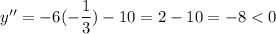`y''=-6(-(1)/(3))-10=2-10=-8<0` maximum

For
`x=-3`,

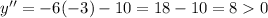`y''=-6(-3)-10=18-10=8>0` minimum

So, the given equation has local maximum at x=-1/3 and the maximum value is

`y=-(-(1)/(3))^3-5(-(1)/(3))^2-3(-(1)/(3))+9\approx 9.48`

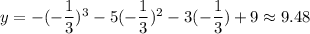
The local maximum at (-0.33,9.48).

Hence, the correct option is A.