Answer:
B
Explanation:
We begin with the given function
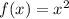
To find
 , we can plug
, we can plug
 into the function
into the function
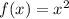
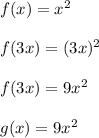
Now that we know the equation of
 , we can find the graph that is equivalent to it.
, we can find the graph that is equivalent to it.
The only graph that is even close to the function
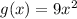 is B, so that is our answer.
is B, so that is our answer.