Answer:
See below.
Explanation:
We have:
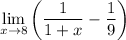
Simply plug in each value:
When x = 7.9,
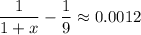
When x = 7.99,

When x = 7.999,
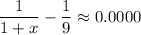
When x = 8.001,
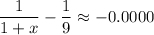
When x = 8.01,
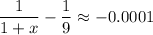
And when x = 8.1,
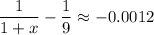
From this pattern, we can conclude that:

Since as the limit approaches 8, the value gets smaller and smaller and approaches zero.
Graphing this, we can confirm our answer.