Question

La parábola que representa la siguiente función: y = mx2 + nx + -1, pasa por los puntos P1 (0, -1) ,P2 (-1,5) y P3 (1,-3). Halle el vértice de la función

Answer 1

El vértice de la función
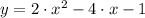`y = 2\cdot x^(2) - 4\cdot x -1` es (1, -3).

Step-by-step explanation:

Toda parábola con eje de simetría paralelo al eje de la variable dependiente se representa por el siguiente polinomio:

`y = a\cdot x^(2) + b\cdot x + c`

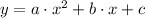
Donde a, b y c son las constantes del polinomio, así como x y y son las variables independiente y dependiente, respectivamente. Algebraicamente hablando, se requiere conocer tres puntos para obtener la ecuación particular por resolución de las constantes del polinomio. Esto es:

`P_(1) (x,y) = (0,-1)`

`-1 = c`

`P_(2) (x,y) = (-1,5)`

`5 = a -b + c`

`P_(3)(x,y) = (1,-3)`

`-3 = a + b + c`

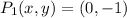
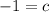
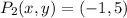
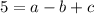
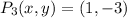
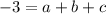
La solución del sistema de ecuaciones lineales es:

`a = 2`,
`b = -4`,
`c = -1`

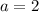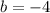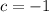
La ecuación de la parábola es
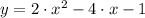`y = 2\cdot x^(2) - 4\cdot x -1`. Ahora, la ecuación estándar de la parábola tiene la siguiente forma:

`y - k = C \cdot (x-h)^(2)`

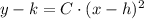
Donde:

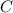`C` - Constante de vértice, adimensional. C > 0 si el vértice es un mínimo absoluto y C < 0 si es un máximo absoluto.

`h`,
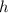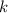`k` - Componentes horizontal y vertical de la ubicación del vértice, adimensionales.

Se transforma el resultado anterior a la forma estándar por métodos algebraicos:

i)
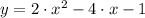`y = 2\cdot x^(2) - 4\cdot x -1` Dado

ii)
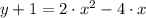`y + 1 = 2\cdot x^(2)-4\cdot x` Compatibilidad con la adición/Existencia de Inverso Aditivo/Conmutatividad de la adición/Modulatividad de la adición.

iii)
`y+1 = 2\cdot [x^(2)-2\cdot x +1 +(-1)]` Modulatividad de la adición/Compatibilidad con la adición/Existencia del Inverso Aditivo.

iv)
`y+1 = 2\cdot [(x-1)^(2)-1]` Asociatividad de la adición/Trinomio cuadrado perfecto.

v)
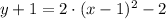`y+1 = 2\cdot (x-1)^(2) - 2` Distributividad de la multiplicación con respecto a la adición/Multiplicación.

vi)
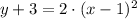`y+3 = 2\cdot (x-1)^(2)` Compatibilidad con la adición/Existencia del Inverso Aditivo/Modulatividad de la adición. Resultado.

Tras revisar directamente en el resultado, se encuentra que el vértice de la función es (1, -3).