Answer:
178.15524 rpm
Step-by-step explanation:
The first thing we want to do is see what information we are given here. This first bit states that both arms and hands together account for 13% of a person's mass. Respectively the head accounts for 7 percent, and the trunk and legs account of 80% of the mass. We have three key points here so far. The mass of the skater is 70 kilograms, having a height of 1.60 meters, arms that are 66 cm, and a trunk diameter of 33 cm. And of course, the initial angular speed of the skater ( ω ) is 68 reps per minute -
{ Total mass of skater (
 ) = 70 kg, }
) = 70 kg, }
{ Height of skater (
 ) = 1.60 m, }
) = 1.60 m, }
{ Diameter of trunk (
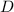 ) = 33 cm = 0.33 m, }
) = 33 cm = 0.33 m, }
{ Length of arms (
 ) = 66 cm = 0.66 m, }
) = 66 cm = 0.66 m, }
{ Mass of Arms and hand (
 ) = 13%( 70 ) = 9.1 kg, }
) = 13%( 70 ) = 9.1 kg, }
{ Mass of Head (
 ) = 7%( 70 ) = 4.9 kg, }
) = 7%( 70 ) = 4.9 kg, }
{ Mass of Trunk and legs (
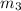 ) = 80%( 70 ) = 56, }
) = 80%( 70 ) = 56, }
{ Initial Angular Speed of Skater ( ω ) = 68 rpm }
______
Take a look at the formula( s ) in the attachments. The first attachment represents the initial moment of inertia of the skater, and the second represents the final moment of inertia of the skater. In other words, when the person's arms are outstretched, and when the arms are parallel to the trunk. Let's calculate each -
Arms outstretched
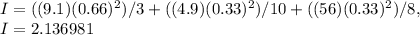
Arms parallel to truck

______
The final angular velocity should be the division of the two multiplied by the number of rpm -
2.136981 / 0.815661( 68 rpm )...
( About ) 178.15524 rpm
Do double check my calculations!