Question

Un tubo de acero de 40000 kilómetros forma un anillo que se ajusta bien a la circunferencia de la tierra. Imagine que las personas junto a él respiran para calentarlo con su aliento y aumentar su temperatura 1 grado Celsius. El tubo se hace más largo. También ya no queda ajustado. ¿A qué distancia sube sobre sobre el nivel del suelo? (solo tomar en cuenta la expansión radial al centro de la tierra, y aplicar la fórmula geométrica que relaciona la circunferencia C con el radio r: C= 2πr).

Answer 1

Step-by-step explanation:

Un tubo de acero de 40000 kilómetros forma un anillo que se ajusta bien a la circunferencia de la tierra. Imagine que las personas junto a él respiran para calentarlo con su aliento y aumentar su temperatura 1 grado Celsius. El tubo se hace más largo. También ya no queda ajustado. ¿A qué distancia sube sobre sobre el nivel del suelo? (solo tomar en cuenta la expansión radial al centro de la tierra, y aplicar la fórmula geométrica que relaciona la circunferencia C con el radio r: C= 2πr).

Answer 2

82.76m

Step-by-step explanation:

In order to find the distance of the steel ring to the ground, when its temperature has raised by 1°C, you first calculate the radius of the steel tube before its temperature increases.

You use the formula for the circumference of the steel ring:

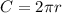`C=2\pi r` (1)

C: circumference of the ring = 40000 km = 4*10^7m (you assume the circumference is the length of the steel tube)

you solve for r in the equation (1):

`r=(C)/(2\pi)=(4*10^7m)/(2\pi)=6,366,197.724m`

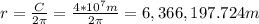
Next, you use the following formula to calculate the change in the length of the tube, when its temperature increases by 1°C:

`L=Lo[1+\alpha \Delta T]` (2)

L: final length of the tube = ?

Lo: initial length of the tube = 4*10^7m

ΔT = change in the temperature of the steel tube = 1°C

α: thermal coefficient expansion of steel = 13*10^-6 /°C

You replace the values of the parameters in the equation (2):

`L=(4*10^7m)(1+(13*10^(-6)/ \°C)(1\°C))=40,000,520m`

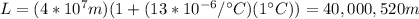
With the new length of the tube, you can calculate the radius of a ring formed with the tube. You again solve the equation (1) for r:

`r'=(C)/(2\pi)=(40,000,520m)/(2\pi)=6,366,280.484m`

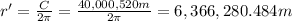
Finally, you compare both r and r' radius:

r' - r = 6,366,280.484m - 6,366,197.724m = 82.76m

Hence, the distance to the ring from the ground is 82.76m