Answer:
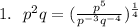
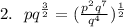
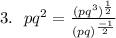
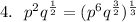
Explanation:
Required
Match each expression to their simplified form
1.
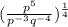
Simplify the expression in bracket by using the following law of indices;
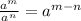
The expression becomes
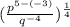


Split the fraction in the bracket
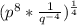
Simplify the fraction by using the following law of indices;
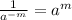
The expression becomes
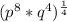
Further simplify the expression in bracket by using the following law of indices;
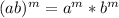
The expression becomes


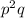
Hence,

2.
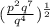
Simplify the expression in bracket by using the following law of indices;
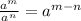
The expression becomes
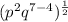
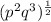
Further simplify the expression in bracket by using the following law of indices;
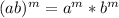
The expression becomes
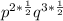
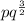
Hence,
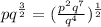
3.
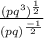
Simplify the numerator as thus:
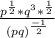
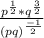
Simplify the denominator as thus:
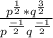
Simplify the expression in bracket by using the following law of indices;
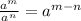
The expression becomes
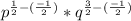
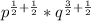
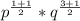

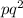
Hence,
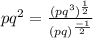
4.
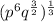
Simplify the expression in bracket by using the following law of indices;
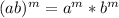
The expression becomes




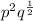
Hence
