Question

List below are the speeds (mi/h) measured from southbound traffic on I-280 near Cupertino, CA. Use the sample data to construct a 99% confidence interval estimate of the population standard deviation: speeds 62, 58, 58, 56, 60, 53, 58

Answer 1

The 99% confidence interval of the population standard deviation is 1.7047 < σ < 7.485

Explanation:

Confidence interval of standard deviation is given as follows;

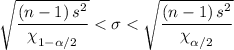
`\sqrt{\frac{\left (n-1 \right )s^(2)}{\chi _(1-\alpha /2)^{}}}< \sigma < \sqrt{\frac{\left (n-1 \right )s^(2)}{\chi _(\alpha /2)^{}}}`

s =
`\sqrt{(\Sigma (x - \bar x)^2)/(n - 1) }`

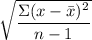
Where:

`\bar x` = Sample mean

s = Sample standard deviation

n = Sample size = 7

χ = Chi squared value at the given confidence level

`\bar x` = ∑x/n = (62 + 58 + 58 + 56 + 60 +53 + 58)/7 = 57.857

The sample standard deviation s =
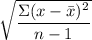`\sqrt{(\Sigma (x - \bar x)^2)/(n - 1) }` = 2.854

The test statistic, derived through computation, = ±3.707

Which gives;

`C. I. = 57.857 \pm 3.707 * (2.854)/(√(7) )`

`\sqrt{(\left (7-1 \right )2.854^(2))/(16.812)^{}}}< \sigma < \sqrt{(\left (7-1 \right )2.854^(2))/(0.872)}`

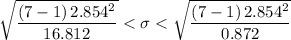
1.7047 < σ < 7.485

The 99% confidence interval of the population standard deviation = 1.7047 < σ < 7.485.