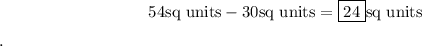Question

What is the area, in square units, of triangle $ABC$ in the figure shown if points $A$, $B$, $C$ and $D$ are coplanar, angle $D$ is a right angle, $AC = 13$, $AB = 15$ and $DC = 5$?

Answer 1

24

Explanation:

Seeing that triangle ACD is a 5-12-13 right triangle, AD=12. Then using Pythagorean Theorem, we can calculate BD to be BD=
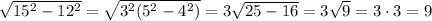`√(15^2-12^2)=√(3^2(5^2-4^2))=3√(25-16)=3√(9)=3 \cdot 3 = 9$`. Thus, the area of triangle ABD is
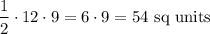`$(1)/(2) \cdot 12 \cdot 9=6 \cdot 9=54 \text{ sq units}$` and the area of triangle ACD is
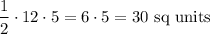`$(1)/(2) \cdot 12 \cdot 5=6 \cdot 5=30 \text{ sq units}$`. The area of triangle ABC is the difference between the two areas:
`$54 \text{sq units} - 30 \text{sq units} = \boxed{24} \text{sq units}$.`

Answer 2

The answer is 24.