Question

List below are the ages (years) of randomly selected race car drivers. Construct a 95% confidence interval estimate of the mean age of all race car drivers: ages 32, 40, 27, 36, 29, 28

Answer 1

The construct of the 95% confidence interval estimate of the mean age of all race car drivers is 26.65 <
`\bar x` < 37.35

Explanation:

The formula for confidence interval (C. I.) for a sample mean is given as follows;

`CI=\bar{x}\pm t_(\alpha/2, n-1) (s)/(√(n))`

Where:

`\bar x` = Sample mean

s = Sample standard deviation

n = Sample size = 6

`t_(\alpha /2)` = The test statistic at the given confidence level

n - 1 = The degrees of freedom 5

The sample mean
`\bar x` = ∑x/n = (32 + 40 + 27 + 36 + 29 + 28)/6 = 32

The standard deviation is given as follows;

`s = \sqrt{(\Sigma (x - \bar x)^2 )/(n - 1) } = 5.099`

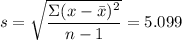
At 95% confidence level, α = 0.05, therefore α/2 = 0.025 and we look for
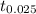`t_(0.025)` and 5 degrees of freedom,
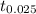`t_(0.025)` = 2.571

When we put in the values, we have;

`CI=32\pm 2.571 * (5.099)/(√(6))`

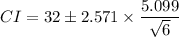
Which gives;

26.65 <
`\bar x` < 37.35

The construct of the 95% confidence interval estimate of the mean age of all race car drivers = 26.65 <
`\bar x` < 37.35.