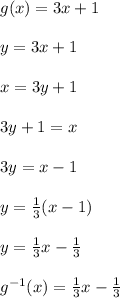Question

F (X) = x² - 2x and 6(x) = 3x+1

A) Find F(g(-4))
B) Find F(g(x)) simply
C) find g^-1 (x)

Answer 1

Part A

g(x) = 3x+1

g(-4) = 3(-4)+1 ... every x replaced with -4

g(-4) = -12+1

g(-4) = -11

Plug this into the f(x) function

f(x) = x^2 - 2x

f( g(-4) ) = (g(-4))^2 - 2( g(-4) )

f( g(-4) ) = (-11)^2 - 2(-11)

f( g(-4) ) = 121 + 22

f( g(-4) ) = 143 is the answer

====================================================

Part B

Plug the g(x) function into the f(x) function

f(x) = x^2 - 2x

f( g(x) ) = ( g(x) )^2 - 2( g(x) ) ... replace every x with g(x)

f( g(x) ) = (3x+1)^2 - 2(3x+1)

f( g(x) ) = (9x^2+6x+1) + (-6x-2)

f( g(x) ) = 9x^2+6x+1-6x-2

f( g(x) ) = 9x^2-1 is the answer

Note that we can plug x = -4 into this result and we would get

f( g(x) ) = 9x^2-1

f( g(-4) ) = 9(-4)^2-1

f( g(-4) ) = 9(16)-1

f( g(-4) ) = 144-1

f( g(-4) ) = 143 which was the result from part A

====================================================

Part C

Replace g(x) with y. Then swap x and y. Afterward, solve for y to get the inverse.

`g(x) = 3x+1\\\\y = 3x+1\\\\x = 3y+1\\\\3y+1 = x\\\\3y = x-1\\\\y = (1)/(3)(x-1)\\\\y = (1)/(3)x-(1)/(3)\\\\g^(-1)(x) = (1)/(3)x-(1)/(3)\\\\`