Answer:
Option C is correct.
Explanation:
Your solution is correct. Given the integral
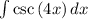 , let y = 4x, du = 4dx, respectively
, let y = 4x, du = 4dx, respectively
 du = dx. Rewrite the given using these values of u and du.
du = dx. Rewrite the given using these values of u and du.
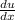 = 4 / 1 = 4,
= 4 / 1 = 4,
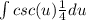 - let us combine csc( u ) and 1 / 4,
- let us combine csc( u ) and 1 / 4,
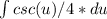 - as 1 / 4 is a constant with respect to u, we can move it out of the integral,
- as 1 / 4 is a constant with respect to u, we can move it out of the integral,
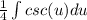 - the integral of csc( u ) with respect to u is present in the form
- the integral of csc( u ) with respect to u is present in the form
"
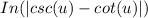 . " Therefore,
. " Therefore,
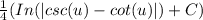 - replace all occurrences of u with 4x to receive the third solution. It can also be written as "
- replace all occurrences of u with 4x to receive the third solution. It can also be written as "
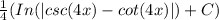 , but only that your move the negative sign to the left of the integral.
, but only that your move the negative sign to the left of the integral.