Answer:
- 0.7
Explanation:
We are given the general quadratic formula, as "
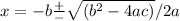 . " This can be represented by two separate formula's, which will come in handy when determining the positive and negative roots of the equation ( and here we need the negative root ):
. " This can be represented by two separate formula's, which will come in handy when determining the positive and negative roots of the equation ( and here we need the negative root ):
1 )
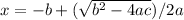 ,
,
2 )

We know that a = 1, b = - 5, and c = - 4 from the equation "
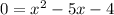 " ( which can be rewritten in the form
" ( which can be rewritten in the form
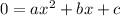 ). Therefore, simply plug in these values into the quadratic formula to receive two solutions:
). Therefore, simply plug in these values into the quadratic formula to receive two solutions:
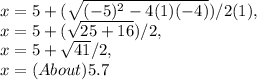 - This is our positive solution
- This is our positive solution
__________
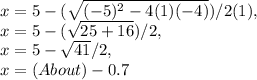 - And this is our negative solution
- And this is our negative solution
You can see that - 0.7 is the negative real number solution to Joline's quadratic equation!