Question

Steam at 5 MPa and 400 C enters a nozzle steadily with a velocity of 80 m/s, and it leavesat 2 MPa and 300 C. The inlet area of the nozzle is 50 cm2, and heat is being lost at a rateof 120 kJ/s. Determine the following:

a) the mass flow rateof the steam.
b) the exit velocity of the steam.
c) the exitarea of the nozzle.

Answer 1

a) the mass flow rate of the steam is
`\mathbf{m_1 =6.92 \ kg/s}`

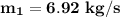
b) the exit velocity of the steam is
`\mathbf{V_2 = 562.7 \ m/s}`

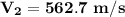
c) the exit area of the nozzle is
`A_2` = 0.0015435 m²

Step-by-step explanation:

Given that:

A steam with 5 MPa and 400° C enters a nozzle steadily

So;

Inlet:

`P_1 =` 5 MPa

`T_1` = 400° C

Velocity V = 80 m/s

Exit:

`P_2 =` 2 MPa

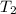`T_2` = 300° C

From the properties of steam tables at
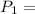`P_1 =` 5 MPa and
`T_1` = 400° C we obtain the following properties for enthalpy h and the speed v

`h_1 = 3196.7 \ kJ/kg \\ \\ v_1 = 0.057838 \ m^3/kg`

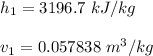
From the properties of steam tables at
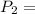`P_2 =` 2 MPa and
`T_1` = 300° C we obtain the following properties for enthalpy h and the speed v

`h_2 = 3024.2 \ kJ/kg \\ \\ v_2= 0.12551 \ m^3/kg`

Inlet Area of the nozzle = 50 cm²

Heat lost Q = 120 kJ/s

We are to determine the following:

a) the mass flow rate of the steam.

From the system in a steady flow state;

`m_1=m_2=m_3`

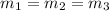
Thus

`m_1 =(V_1 * A_1)/(v_1)`

`m_1 =(80 \ m/s * 50 * 10 ^(-4) \ m^2)/(0.057838 \ m^3/kg)`

`m_1 =(0.4 )/(0.057838 )`

`\mathbf{m_1 =6.92 \ kg/s}`

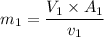
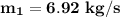
b) the exit velocity of the steam.

Using Energy Balance equation:

`\Delta E _(system) = E_(in)-E_(out)`

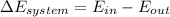
In a steady flow process;

`\Delta E _(system) = 0`

`E_(in) = E_(out)`

`m(h_1 + (V_1^2)/(2))`
`= Q_(out) + m (h_2 + (V_2^2)/(2))`

`- Q_(out) = m (h_2 - h_1 + (V_2^2-V^2_1)/(2))`

`- 120 kJ/s = 6.92 \ kg/s (3024.2 -3196.7 + (V_2^2- 80 m/s^2)/(2)) * ((1 \ kJ/kg)/(1000 \ m^2/s^2))`

`- 120 kJ/s = 6.92 \ kg/s (-172.5 + (V_2^2- 80 m/s^2)/(2)) * ((1 \ kJ/kg)/(1000 \ m^2/s^2))`

`- 120 kJ/s = (-1193.7 \ kg/s + 6.92\ kg/s ( (V_2^2- 80 m/s^2)/(2)) * ((1 \ kJ/kg)/(1000 \ m^2/s^2))`

`V_2^2 = 316631.29 \ m/s`

`V_2 = \sqrt{316631.29 \ m/s`

`\mathbf{V_2 = 562.7 \ m/s}`

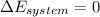
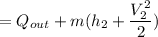
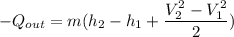
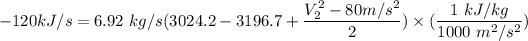
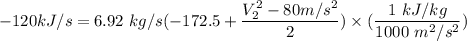
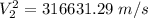
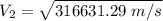
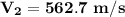
c) the exit area of the nozzle.

The exit of the nozzle can be determined by using the expression:

`m = (V_2A_2)/(v_2)`

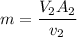
making
`A_2` the subject of the formula ; we have:

`A_2 = ( m * v_2)/(V_2)`

`A_2 = ( 6.92 * 0.12551)/(562.7)`

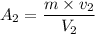
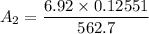
`A_2` = 0.0015435 m²