Answer:
The final speed of the lion-gazelle system immediately after the attack is 69.862 kilometers per hour.
Step-by-step explanation:
Let suppose that lion and Thomson's gazelle are running at constant speed before and after collision and that collision is entirely inelastic. Given the absence of external force, the Principle of Momentum Conservation is applied such that:
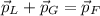
Where:
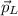 - Linear momentum of the lion, measured in kilograms-meters per second.
- Linear momentum of the lion, measured in kilograms-meters per second.
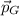 - Linear momentum of the Thomson's gazelle, measured in kilograms-meters per second.
- Linear momentum of the Thomson's gazelle, measured in kilograms-meters per second.
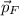 - Linear momentum of the lion-Thomson's gazelle, measured in kilograms-meters per second.
- Linear momentum of the lion-Thomson's gazelle, measured in kilograms-meters per second.
After using the definition of momentum, the system is expanded:
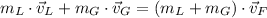
Vectorially speaking, the final velocity of the lion-gazelle system is:

Where:
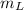 ,
,
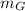 - Masses of the lion and the Thomson's gazelle, respectively. Measured in kilograms.
- Masses of the lion and the Thomson's gazelle, respectively. Measured in kilograms.
 ,
,
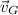 ,
,
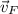 - Velocities of the lion, Thomson's gazelle and the lion-gazelle system. respectively. Measured in meters per second.
- Velocities of the lion, Thomson's gazelle and the lion-gazelle system. respectively. Measured in meters per second.
If
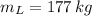 ,
,
 ,
,
![\vec v_(L) = 81.8\cdot j\,\left[(km)/(h) \right]](https://img.qammunity.org/2021/formulas/physics/college/iz2f0ysvu7lovvl6gevppjeyuzh266w3er.png) and
and
![\vec v_(G) = 59.0\cdot i\,\left[(km)/(h) \right]](https://img.qammunity.org/2021/formulas/physics/college/gctpo2o4rfwsqpg792cqagh8yuugytamle.png) , the final velocity of the lion-gazelle system is:
, the final velocity of the lion-gazelle system is:
![\vec v_(F) = (177\,kg)/(177\,kg+32\,kg)\cdot \left(81.8\cdot j\right)\,\left[(km)/(h) \right] + (32\,kg)/(177\,kg+32\,kg)\cdot \left(59.0\cdot i\right)\,\left[(km)/(h) \right]](https://img.qammunity.org/2021/formulas/physics/college/on7wjpgcfy38crkf93b1gr7q86udzwlxf3.png)
![\vec v_(F) = 9.033\cdot i + 69.276\cdot j\,\left[(km)/(h) \right]](https://img.qammunity.org/2021/formulas/physics/college/apc59qvw6soz612a3k57olj1gc8jhgbokh.png)
The speed of the system is the magnitude of the velocity vector, which can be found by means of the Pythagorean theorem:
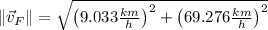
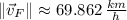
The final speed of the lion-gazelle system immediately after the attack is 69.862 kilometers per hour.