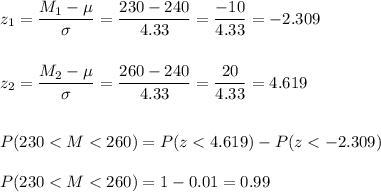Question

People counting calories have to be careful about the estimates placed on prepackaged food. Suppose testing shows that a certain brand of doughnut has a mean calorie count of 240, so that is the amount printed on the package. However, testing shows that the calories counts vary, following a normal distribution with a standard deviation of 15 calories.

A) Find the probability that an individual doughnut for this brand contains more than 275 calories.
B) Find the probability that a random sample of 12 of these doughnuts contains a mean number of calories between 230 and 260.

Answer 1

A) P(X>275) = 0.01

B) P(230<M<260) = 0.99

Explanation:

We have a normal distribution with mean: 240 calories and standard deviation: 15 calories.

To find the probability that an individual doughnut for this brand contains more than 275 calories, we calculate the z-score for X=275 in this normal distribution, and then calculate the probability for this z-score with the standard normal distribution:

`z=(X-\mu)/(\sigma)=(275-240)/(15)=(35)/(15)=2.33\\\\\\P(X>275)=P(z>2.33)=0.01`

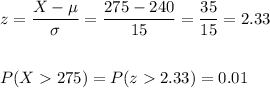
In the case we are talking about a sample mean, we use the standard deviation of the sample distribution.

The standard deviation for the sample means is equal to the standard deviation of the population divided by the square root of the sample size (in this case, n=12). The mean of the sampling distirbution is expected to be equal to the population mean.

`\mu_s=\mu=240\\\\ \sigma_s=(\sigma)/(√(n))=(15)/(√(12))=(15)/(3.4641)=4.33`

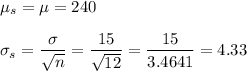
We have to calculate the probability that this sample mean is within 230 and 260.

`z_1=(M_1-\mu)/(\sigma)=(230-240)/(4.33)=(-10)/(4.33)=-2.309\\\\\\z_2=(M_2-\mu)/(\sigma)=(260-240)/(4.33)=(20)/(4.33)=4.619\\\\\\P(230<M<260)=P(z<4.619)-P(z<-2.309)\\\\P(230<M<260)=1-0.01=0.99`