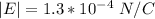Complete Question
The complete question is shown on the first uploaded image (reference for Photobucket )
Answer:
The electric field is
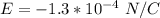
Step-by-step explanation:
From the question we are told that
The linear charge density on the inner conductor is
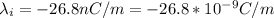
The linear charge density on the outer conductor is
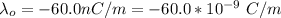
The position of interest is r = 37.3 mm =0.0373 m
Now this position we are considering is within the outer conductor so the electric field at this point is due to the inner conductor (This is because the charges on the conductor a taken to be on the surface of the conductor according to Gauss Law )
Generally according to Gauss Law
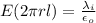
=>
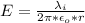
substituting values
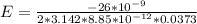
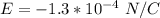
The negative sign tell us that the direction of the electric field is radially inwards
=>