Question

efore the overtime rule in a football league was​ changed, among 400 overtime​ games, 194 were won by the team that won the coin toss at the beginning of overtime. Using a 0.10 significance​ level, use the sign test to test the claim that the coin toss is fair in the sense that neither team has an advantage by winning it. Does the coin toss appear to be​ fair?4

Answer 1

The coin toss does not appear to be fair

Explanation:

From the question we are told that

The sample size is
`n = 400`

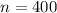
The number of game won by team that won the coin toss at the beginning of overtime
`x = 194`

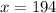
The level of significance is
`\alpha = 0.10`

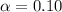
The population proportion is evaluated as

`p = (194)/(400)`

`p = 0.485`

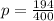
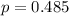
Since the population proportion is 0.485
`\approx` 0.5 which implies that the coin toss is fair then

The Null hypothesis is

`H_o : p = 0.485`

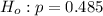
and The Alternative hypothesis is

`H_a : p \\e 0.485`

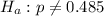
The test statistics is evaluated as follows

`t = ([x + p] - [(n)/(2) ])/((√(n) )/(2) )`

substituting values

`t = ([194 + 0.485] - [(400)/(2) ])/((√(400) )/(2) )`

`t = -0.5515`

=>
`|t| = 0.5515`

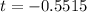
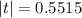
now the critical value of
`\alpha` for a two tail test(it is two tailed because we are test whether the critical value is less than or greater than the test statistics ) is

`t_(\alpha ) = 1.645`

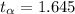
This is usually found from the critical value table

Now comparing the critical values and the calculated test statistics we see that the critical value is greater than the test statistics hence the Null hypothesis is rejected

This means that the coin toss is not fair