Question

In a ballistic pendulum experiment, a small marble is fired into a cup attached to the end of a pendulum. If the mass of the marble is 0.0215 kg and the mass of the pendulum is 0.250 kg, how high h will the pendulum swing if the marble has an initial speed of 5.15 m/s? Assume that the mass of the pendulum is concentrated at its end so that linear momentum is conserved during this collision.

Answer 1

h = 8.48*10^-3m

Step-by-step explanation:

In order to calculate the height reached by the pendulum with the marble, you first take into account the momentum conservation law, to calculate the speed of both pendulum and marble just after the collision.

The total momentum of the system before the collision is equal to the total momentum after:

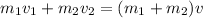`m_1v_1+m_2v_2=(m_1+m_2)v` (1)

Here you used the fact that the pendulum has its total mass concentrated at the end of the pendulum.

m1: mass of the marble = 0.0215kg

m2: mass of the pendulum concentrated at its end = 0.250kg

v1: horizontal speed of the arble before the collision = 5.15m/s

v2: horizontal speed of the pendulum before the collision = 0m/s

v: horizontal speed of both marble and pendulum after the collision = ?

You solve the equation (1) for v, and replace the values of the other parameters:

`v=(m_1v_1+m_2v_2)/(m_1+m_2)\\\\v=((0.0215kg)(5.15m/s)+(0.250kg)(0m/s))/(0.0215kg+0.250kg)=0.40(m)/(s)`

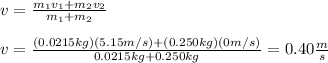
Next, you use the energy conservation law. In this case the kinetic energy of both marble and pendulum (just after the collision) is equal to the potential energy of the system when both marble and pendulum reache a height h:

`U=K\\\\(m_1+m_2)gh=(1)/(2)(m_1+m_2)v^2\\\\h=(v^2)/(2g)`

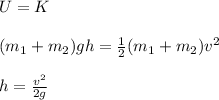
v = 0.40m/s

g: gravitational acceleration = 9,8m/s^2

`h=((0.40m/s)^2)/(2(9.8m/s^2))=8.48*10^(-3)m`

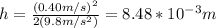
Then, the height reached by marble and pendulum is 8.48*10^-3m