Answers:
n = 288
Yes it is possible to express
 as multiples of the same square root (12 multiples of
as multiples of the same square root (12 multiples of
 )
)
=====================================================
Step-by-step explanation:
Simplify the first part of the left side
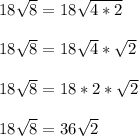
And do the same for the second part of the left side
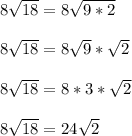
For each simplification, you are trying to factor the stuff under the square root so that you pull out the largest perfect square factor possible.
-------------------------
The original equation
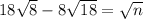 turns into
turns into
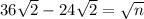
We have the common factor of
 so we can combine like terms on the left side ending up with
so we can combine like terms on the left side ending up with
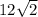
-------------------------
So,

Yes it is possible to express
 as multiples of the same square root. In this case, we can express the left hand side of the original equation as 12 multiples of
as multiples of the same square root. In this case, we can express the left hand side of the original equation as 12 multiples of
