Answer:
The number of minutes of the ride that are spent higher than 15 meters above the ground is 18 minutes.
Explanation:
We will use the sin function for the height of the Ferris wheel.
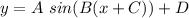
A = amplitude
C = phase shift
D = Vertical shift
2π/B = period
From the provided information:
A = 15/2 = 7.5 m
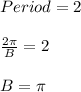
Compute the Vertical shift as follows:
D = A + Distance of wheel from ground
= 7.5 + 1
= 8.5
The equation of height is:
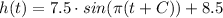
Now at t = 0 the height is, h (t) = 1 m.
Compute the value of C as follows:
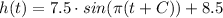
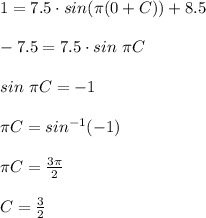
So, the complete equation of height is:
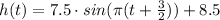
Compute the number of minutes of the ride that are spent higher than 15 meters above the ground as follows:
h (t) ≥ 15
![h(t)=15\\\\7.5\cdot sin(\pi (t+(3)/(2)))+8.5=15\\\\7.5\cdot sin(\pi (t+(3)/(2)))=6.5\\\\sin(\pi (t+(3)/(2)))=(6.5)/(7.5)\\\\(\pi (t+(3)/(2)))=sin^(-1)[(13)/(15)]\\\\\pi (t+(3)/(2))=60.074\\\\t+(3)/(2)=19.122\\\\t=17.622\\\\t\approx 18](https://img.qammunity.org/2021/formulas/mathematics/high-school/t5ccb417fwk6nvrfdrjtkg6phc4kv66e1x.png)
Thus, the number of minutes of the ride that are spent higher than 15 meters above the ground is 18 minutes.