Question

If 40.0 g of molten iron(II) oxide reacts with 10.0 g of mag-nesium, what is the mass of iron produced

Answer 1

`m_(Fe)=23.0gFe`

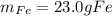
Step-by-step explanation:

Hello,

In this case, the undergoing chemical reaction is:

`FeO+Mg\rightarrow Fe+MgO`

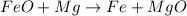
Thus, for the given masses of reactants we should compute the limiting reactant for which we first compute the available moles of iron (II) oxide:

`n_(FeO)=40.0gFeO*(1molFeO)/(72gFeO) =0.556molFeO`

Next, we compute the consumed moles of iron (II) oxide by the 10.0 g of magnesium, considering their 1:1 molar ratio in the chemical reaction:

`n_(FeO)^(consumed)=10.0Mg*(1molMg)/(24.3gMg)*(1molFeO)/(1molMg)=0.412molFeO`

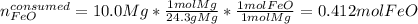
Therefore, we can notice there is less consumed iron (II) oxide than available for which it is in excess whereas magnesium is the limiting reactant. In such a way, the produced mass of iron turns out:

`m_(Fe)=0.412molFeO*(1molFe)/(1molFeO)*(56gFe)/(1molFe)\\ \\m_(Fe)=23.0gFe`

Regards.