Complete question:
A force F is applied to the block as shown (check attached image). With an applied force of 1.5 N, the block moves with a constant velocity.
Approximately what applied force is needed to keep the box moving with a constant velocity that is twice as fast as before? Explain
Answer:
The applied force that is needed to keep the box moving with a constant velocity that is twice as fast as before, is 3 N
Force is directly proportional to velocity, to keep the box moving at the double of initial constant velocity, we must also double the value of the initially applied force.
Step-by-step explanation:
Given;
magnitude of applied force, F = 1.5 N
Apply Newton's second law of motion;
F = ma
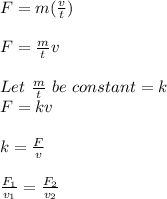
The applied force needed to keep the box moving with a constant velocity that is twice as fast as before;
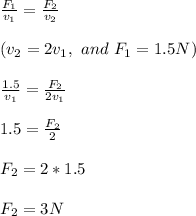
Therefore, the applied force that is needed to keep the box moving with a constant velocity that is twice as fast as before, is 3 N
Force is directly proportional to velocity, to keep the box moving at the double of initial constant velocity, we must also double the value of the applied force.