Question

An automotive salesman determines that he has a 36​% chance of selling a car to a random customer at his dealership. A group of eight customers is chosen at random. The salesman determines the probability of an event is as follows. (Start 2 By 1 Matrix 1st Row 1st Column 8 2nd Row 1st Column 3 EndMatrix )0.36 cubed 0.64 Superscript 5 Baseline plus (Start 2 By 1 Matrix 1st Row 1st Column 8 2nd Row 1st Column 2 EndMatrix )0.36 squared 0.64 Superscript 6 What does this probability​ represent? Choose the correct answer below. A. The probability represents exactly three or two customers buying a car. B. The probability represents more than two customers buying a car. C. The probability represents exactly three or two customers not buying a car. D. The probability represents less than three customers buying a car.

Answer 1

The correct option is (A).

Explanation:

Let the random variable X represent the number of cars sold by the automotive salesman.

It is provided that the probability of the salesman selling a car to a random customer at his dealership is, p = 0.36.

A random sample of n = 8 customers is chosen.

The events that a customer purchases a car is independent of the other customers.

The random variable X thus follows a Binomial distribution with parameters n = 8 and p = 0.36.

The probability mass function of X is:

`P(X=x)={8\choose x}(0.36)^(x)(0.64)^(8-x);\ x=0,1,2,3...`

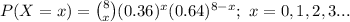
The probability of an event is provided as follows:

`{8\choose 3}(0.36)^(3)(0.64)^(5)+{8\choose 2}(0.36)^(2)(0.64)^(6)`

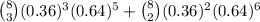
The probability represents exactly three or two customers buying a car.