Question

You’re standing at the highest point on the Moon, 10,786 mm above the level of the Moon’s mean radius. You’ve got a golf club and a golf ball.

Part A

(How fast would you need to hit the ball horizontally so it goes into a circular orbit?)

Express your answer with the appropriate units.

Part B

(If you hit the ball vertically with the same speed, to what height above you would it rise?)

Express your answer with the appropriate units.

Answer 1

A) v = 1,675 10³ m / s , B) r₂ = 11,673 10⁶ m

Step-by-step explanation:

A) This exercise we must use Newton's second law, where the forces of gravity are the Moon

F = m a

acceleration is centripetal

a = v² / r

force is the force of universal attraction

F = G m M / r²

we substitute

G m M / r² = m v² / r

v² = G M / r

distance

r = R_moon + h

r = 1.74 10⁶ +1.0786 10⁴

r = 1,750786 10⁶ m

we calculate

v = √ (6.67 10⁻¹¹ 7.36 10²² / 1.75 10⁶)

v = √ (2,8052 10⁶)

v = 1,675 10³ m / s

B) let's use energy conservation

Starting point. In the mountain

Em₀ = K + U = ½ m v² + G m M / r

Final point. Where the speed is zero

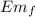`Em_(f)` = U = G mM / r₂

Em₀ = Em_{f}

½ m v² + G m M / r = G mM / r₂

1 / r₂ = (½ v₂ + G M / r) / GM

let's calculate

1 / r₂ = (½ (1,675 10³)² + 6.67 10⁻¹¹ 7.36 10²² / 1.75 10⁶) /(6.67 10⁻¹¹ 7.36 10²²)

1 / r₂ = (1,4028 10⁶ + 2,805 10⁶) / 49.12 10¹¹

1 / r₂ = 8.5664 10⁻⁷

r₂ = 11,673 10⁶ m